Lecture 1: Introduction
\( \newcommand{\abs}[1]{\left\lvert#1\right\rvert} \newcommand{\ceiling}[1]{\lceil#1\rceil} \)Administrivia
Please note all of the information found on the course Home Page and Policies Page, which are included here by reference. Note specifically the policy on Academic Honesty, as every year there are CS students who get this wrong, and suffer significant academic consequences. Don't be one of them. Also note "How to succeed in CMSC-16100 (and College)" on the course home page.
Getting started
You should set up the Glasgow Haskell system. The easy way is to download your platform specific Haskell Platform installer from http://hackage.haskell.org/platform, and follow the instructions. Chose the "Download Full." If you pursue programming in Haskell, you may want to consider minimal downloads in the future, but it would be a complication now. Today's lab will include an install party—if you have a laptop, bring it to lab.
Homework Standards, v. 1.0
- Make sure your name, and the exercise number are clearly shown on the homework. For code exercises, it is most convenient to do this via a comment at the top of the file.
- Type your homework and use a monospace font (i.e. Courier, Consolas, Monaco) at an easily legible size for code.
- Submit your homework on 8.5" x 11", unperforated, paper.
- For programming exercises, your solutions should include
Haskell source files, not just commands issued in the interactive
ghci interpreter.
- Do provide sample runs, when feasible, and these will often involve interaction with the interpreter.
- Include a type declaration for all top-level defined names.
Don't worry yet if this doesn't all make sense. It should by the end of the day.
Haskell
Haskell is a strongly-typed, lazy, pure, functional language. We'll get around to defining these terms in due course, but suffice it to say that this is not your father's FORTRAN, nor even the Java or C++ you might have learned in High School. In traditional procedural programming language, programs are compiled (i.e., translated) into a sequence of instructions for manipulating memory; whereas in functional languages, computation can be understood as the mathematical process of disciplined substitution. Programming in Haskell often feels like “programming with mathematics.”
Our decision to teach Haskell may seem peculiar, idiosyncratic, and perhaps even iconoclastic. Students who favor languages that are more familiar to them, and more important in the here-and-now commercially, often feel that way. We don't want to get into a debate over our choices today, but instead will lay out our priorities, and ask you to suspend disbelief. A useful metaphor, drawn from hockey (this is a hockey town), is “skating to where the puck is going to be.” Time and again, we have seen features, concepts, and even idioms of Haskell taken up by more traditional languages. Our goal is to prepare you for the future, and Haskell's the best vehicle we know for doing so.
The Past
“The past is never dead. It's not even past.”
William Faulkner
Early attempts to formalize mathematics ran into a variety of paradoxes, i.e., self-contradictory statements. One such was Russell's Paradox, in which Bertrand Russell defined the set
$$R = \{x \mathbin{\vert} x \not\in x\},$$using Frege's axiom of comprehension, which allows one to create a set out of the sets that satisfy some predicate. The paradox comes from asking whether or not $R \in R$. This reduces, by the definition of $R$, to
$$R \in R \iff R \not\in R,$$a self-contradictory statement, a paradox.
There were several distinct approaches developed used to avoid Russell's paradox.
The most influential approach was Ernst Zermelo's, in which comprehensions defined classes rather than sets, and where the intersection of a class with a set is also a set. As only sets can be elements of classes or sets, and one can conclude that $R$ is a proper class, i.e., a class which is not a set, and thereby resolve the contradiction.
Another approach was Russell-Whitehead's theory of ramified types, which required assigning an integer to each variable used in forming a statement, e.g., we'll use the notation $x::i$ to mean that the variable $x$ is given the type (integer) $i$. These types had to be used consistently, i.e., if we used both $x::i$ and $x::j$ in an expression, then we must have $i=j$. They then restricted the use of $\in$ to be strictly monotonic in type, i.e., $(x::i) \in (y::j)$ could be formed only if $i\lt j$. This resolves the paradox by making the comprehension $(x::i) \in (x::i)$ at the core of Russell's paradox syntactically invalid, as no integer $i$ can be chosen to meet the constraint $i \lt i$.
A first impression is that the theory of ramified types is ad hoc; it gets around Russell's paradox by a seeming “magic bullet” that allows us to ignore it. But at a deeper and more sympathetic level, the ramified theory of types prevents circularities in the use of $\in$, by insisting on definitions in which the use of $\in$ is “well-founded in type.”
In practice, mathematicians use set theory as a foundational abstraction, and further abstractions get built out of sets. For example, certain sets represent natural numbers, $0 = \emptyset$, $1 = \{0\}$, $2=\{0,1\}$, etc. But once we get beyond foundational concerns, we tend to reason directly using the higher abstractions, and not to worry about the sets that represent them (although mathematicians can't stop themselves from using coincidences of representation as notational puns). Thus, “natural number” can be thought of as a type in a slightly different sense, as both an abstraction in its own right, but also an interpretation of the meaning of certain sets.
Computers and Programming
Computers are complex devices. We use them to write papers, run spreadsheets, store and manipulate photos and videos, to play games, etc. And their design and construction is likewise complex. Yet at their mathematical core, computers rest on very simple ideas, e.g., a bit is logical element that can be in one of two distinct states (on/off, 0/1, true/false). The processor, in a step-wise fashion, changes the value contained in some bits in a lawful way based on the values contained in other bits. Bits are to computers as sets are to mathematics—the foundation upon which all other representations are built.
Types enter programming as means of interpretations of various collections of bits, e.g., these bits represent an account balance, those bits represent a photograph, those other bits represent a telephone number. Programming often involves building representations of new types out of the representations of old types, and the defining manipulations of values of those new types in terms of manipulations of the values of old types.
Traditional Programming Languages
In traditional compiled languages like C, C++, and Java, we declare types for every name used in a program. The compiler infers the type of every expression, in a strict bottom-up way (the type of an expression is defined by the types of its constituent parts). In doing so, the compiler enforces the consistent use of these names, e.g., typically you can't add an integer to a floating-point number, but must first convert one to the type of another.
A problem, especially with older languages, is that their type systems were inflexible, which often meant that code either had to be duplicated to work at different types (and duplicated code is a bad thing), or that various nefarious tricks had to be used to get the type system to accept code taht couldn't be typed, mooting the point of having a type system at all.
Scripting Languages
“There are three great virtues of a programmer: laziness, impatience, and hubris.”
Larry Wall
For doing quick-and-dirty programming, traditional programming languages often offend programmers who exhibit Wall's three great virtues. The discipline of declaring types for all names offends their laziness. The time required for compilation offends their sense of impatience. And the idea that their use of the language is constrained by the compiler's need to ensure consistent usage offends their hubris. And so, scripting languages like Perl and Python eschew a static type-discipline, in favor of dynamic runtime type-checking, and interpretation (which typically has shorter latencies, and facilitates dynamic loading) over compilation.
To make this work, the values stored in memory have to encode their type, and these types have to be checked at run time to select appropriate implementations of various operations, or to produce an error if no such implementation exists. To facilitate rapid development, these languages will often convert types “on the fly” as needed to make sense of a programming construct, e.g., if you try to add an integer to a floating point number in Python, the integer will first be converted into a floating-point number, and then the two floating point numbers will be added. A problem is that the specific coercions may not be expected or desired, cf., courtesy of xkcd:
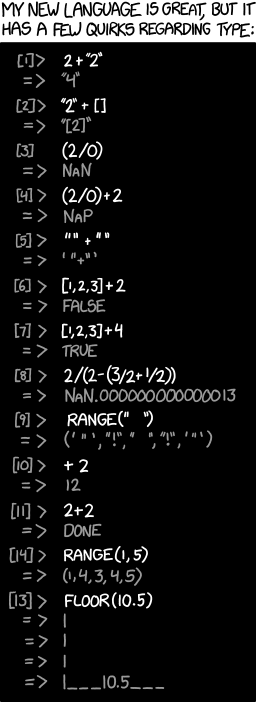
But this happens automatically, and so panders to the laziness and impatience of the programmer, and sometimes spares them the consequences of their hubris, when the latter is ill-founded. The problem with this is the weasel word “sometimes.”
Scripting programmers are confident in their own ability to reason about the actual types that will be encountered in these at runtime, and so are confident that operations will only be called with appropriate and compatible arguments. The right word for this is hubris. In practice, many bugs in scripting language programs are revealed through runtime type incompatibilities, which exposes that their programmer's confidence has been misplaced. Moreover, code often requires debugging, and is subsequently maintained, often not by the original programmer. Code is fragile, in the sense that small changes can invalidate these chains of reasoning about type usage, and those chains of reasoning are often not available when code is being reworked.
Sooner or later, an end user encounters a runtime error when the code tries to multiply 'dirt' times 'curtains' or some such, and no one can figure out how something quite so absurd came to be.
Haskell's Approach to Types
“Computers should think, and people should play.”
Carl Smith
Haskell uses a strong, flexible type system. Moreover, it makes widespread use of powerful type inference algorithms that moot the need for most type declarations. This isn't to say that Haskell programmers don't include type declarations, but rather that the declarations tend to serve a different function: they're a compiler verified “comment,” comprising a contract about name use.
Let's consider some examples, from within the ghci Haskell interpreter:
$ ghci
GHCi, version 8.2.1: http://www.haskell.org/ghc/ :? for help
Prelude> 1 :: Integer
1
This is pretty easy stuff. We're asking the interpreter to evaluate the expression 1, and telling it that the result should be of type Integer. [Note that the Integer type is infinite-precision.] Haskell does not actually need the type annotation, cf.,
Prelude> 1
1
This is all very simple. We can see a subtle distinction if we ask Haskell to evaluate 1, but telling it that the result should be a floating-point number:
Prelude> 1 :: Double
1.0
The 1 is a numeric literal, i.e., a bit of syntax that can be interpreted as a number, and that Double is the typical type used to represent floating-point values. Moreover, when Haskell prints a Double, it always includes a decimal point with at least one fractional digit.
If we look more deeply still, we can ask Haskell for the type of 1, and we get a surprisingly complicated answer:
Prelude> :t 1
1 :: Num p => p
What this tells us is that 1 is an expression which has some type p which is an instance of the Num type class.

There's a lot going on here! But the point is that when asked Haskell to evaluate 1 :: Integer, Haskell first had to verify that Integer is an instance of Num, and then use capabilities of the Integer type that all instances of type class Num are required to provide. Likewise, when we asked Haskell to evaluate 1 :: Double, Haskell first had to verify that Double is an instance of Num, and then use capabilities of the Double class that all instances of type class Num are required to provide. In this case, the chain of reasoning went top-down, although since there's only one level, it's a bit tricky to see. Let's consider a more complex example.
Prelude> 2 + 3 :: Integer
5
This is deceivingly simple. We're asking Haskell to evaluate the expression 2 + 3, producing an Integer. A first bit of complexity here is the use of infix addition. Haskell permits us to use various infix operators, and this is a great notational convenience, but the type system is actually assumes prefix operators, and so the expression 2 + 3 is translated to (+) 1 2, where (+) is the syntax for binary addition written in prefix form. We want this whole expression to have the type Integer, and so we have to consider the type of (+) which is Num a => a -> a -> a.

At this point, it should be clear that the language of types is also an expression language, albeit with different operators. What this means is that for any type n which is an instance of the Num type class, (+) is a function that takes two arguments of type n, and produces a result of type n. [Note that we're telling a bit of a white lie here, which we'll deal with in an upcoming lecture.] Since Haskell knows that the result is supposed to be of type Integer, it must first check that Integer is an instance of Num (which it is), and then it can infer that the arguments are of type Integer also. This enables it to interpret 1 and 2 appropriately as numeric literals that represent Integer values.
Haskell uses a similar line of reasoning to handle
Prelude> 2 + 3 :: Double
5.0
Albeit, with a visible difference due to the way Haskell prints floating point numbers.
Still, the Haskell type system has done such a good job of working invisibly behind the scenes that we might wonder why it is there at all. So let's break things. Consider
Prelude> (2 :: Integer) + 3 :: Double
What could possibly go wrong?
We're asking Haskell to add 2, considered as a value of type Integer, to some value represented by the numeric literal 3, obtaining a result that's a Double. This is a conundrum for (+) :: Num a => a -> a -> a. The type constraint on its first argument requires that a be interpreted as Integer, whereas the overall type constraint on the expression requires that a be interpreted as Double, and these are different types! Indeed, that's what the error message we get back from ghci says:
<interactive>:14:1: error:
• Couldn't match expected type ‘Double’ with actual type ‘Integer’
• In the expression: (2 :: Integer) + 3 :: Double
In an equation for ‘it’: it = (2 :: Integer) + 3 :: Double
This brings up an important point. Compiler error messages can be long and scary. They're long because the compiler writer doesn't know exactly what information you need to figure out what's wrong, and so they tend to err on the side of giving you too much information, and they're scary because you won't necessarily know how to interpret all of that information, and there's a tendency to assume that because the compiler thought it mattered, you should too.
The first line tells us where the error occurred, in this case, in an interactive session, on the fourteenth line, at the first character position. This is TMI for now, but localization is crucial when our programs are spread out over multiple, long files. The second line tells us about the error: at some point, our code seems to require that Double and Integer are the same type, an inconsistency. The third line consists of the expression whose type analysis failed, and the fourth provides a bit more context, and hints at some capabilities of the interpreter we haven't yet learned.
* Exercise 1.1 Consider the expression (1 :: Integer) + 2 * (3 :: Double). This will cause a type error, because the two different type constraints are inconsistent. One bit of trickiness is that the inconsistency could be revealed either in the analysis of (+) or (*). Provide both analyses.
A Taste of Programming
The process for programming in Haskell typically involves writing code in a Haskell Source file, which will typically have the extension .hs. Note that these code files must be plain text files (which is to say, you can't edit them using MS Word or similar word-processing programs). More complex will require the use of the cabal build system, and likely source control systems such as git. We'll learn about these tool later, and for now can rely on a simpler process.
Let's suppose we want to be able to compute the length of the hypotenuse of a right triangle, given the lengths of the sides. We know the pythagorean theorem from our high school math classes. Given a right triangle

the sides $a$, $b$, and $c$ are related by the formula $a^2 + b^2 = c^2$. A quick reorganization of this formula gives us $$c = \sqrt{a^2 + b^2},$$ which determines $c$ as a function of $a$ and $b$, and which can be easily expressed as code.
-- Hypotenuse.hs
hypotenuse a b = sqrt (a^2 + b^2)
This is a simple Haskell source file. The first line is a comment, identifying this as the file Hypotenuse.hs. Comments are annotations we make to the code that the compiler doesn't interpret, but may help future readers (most likely, us!) understand something about the code. The third line defines hypotenuse to be a function that takes two arguments, and computes a value based on them. Assuming we've done this correctly, we can load this file into ghci:
Prelude> :l Definitions
[1 of 1] Compiling Main ( Hypotenuse.hs, interpreted )
Ok, 1 module loaded.
*Main>
The change in prompt isn't important, but we've now added a new function to our system, and that is:
*Main> hypotenuse 3 4
5.0
At this point, we might consider ourselves done. But... real Haskell programmers wouldn't be happy leaving things here, and your instructors and graders won't be happy if you do. Haskell programmers understand laziness much more deeply than Perl programmers, both as a language evaluation strategy, and as attribute of good programming. In particular, avoiding a little bit of disciplined work now, at the risk of having to do much more in the future isn't lazy, it's a self-defeating strategy that costs us unnecessary work over time. So we'll start by adding a module declaration to our program, and some specially formatted comments that will save us time later in using this code.
-- | A module for working with triangles.
module Hypotenuse where
-- | Compute the length of the hypotenuse of a triangle from the lengths
-- of its sides.
hypotenuse a b = sqrt (a^2 + b^2)
Note that as University of Chicago students, we expect that your comments will be clear and eloquent in their own right, with correct spelling, grammar, and punctuation. It is often said that, “Documentation is the armpit of the industry.” We can do better. You will do better.
These are Haddock comments, and are used to create Haskell Documentation. Note an ordinary comment begins with a double-hyphen --, whereas a Haddock comment adds a space and a vertical bar -- |. The first comment describes the purpose of the module, which typically consists of a number of related definitions, and the comment before the definition of hypotenuse describes its intended meaning/use. If we load this, we'll see a minor difference in ghci's prompts:
$ ghci Hypotenuse
GHCi, version 8.2.1: http://www.haskell.org/ghc/ :? for help
[1 of 1] Compiling Hypotenuse ( Hypotenuse.hs, interpreted )
Ok, 1 module loaded.
*Hypotenuse>
Note how the module name is now incorporated in the prompt.
It is conventional to declare the types of all names defined at the top-level. This requires that we figure out what the type of hypotenuse actually is. Fortunately, the compiler has already done this for us, and we can ask:
*Hypotenuse> :t hypotenuse
hypotenuse :: Floating a => a -> a -> a
At this point, we have a choice. We can simply copy the type that Haskell has computed for us back to our source file, or we can chose a more restrictive type. Let's say, for the sake of argument, that we're confident that we'll only use this with Double values. We add the appropriate type declaration our source file as follows:
-- | A module for working with triangles.
module Hypotenuse where
-- | Compute the length of the hypotenuse of a triangle from the lengths
-- of its sides.
hypotenuse :: Double -> Double -> Double
hypotenuse a b = sqrt (a^2 + b^2)
And then reload our source
*Hypotenuse> :r
[1 of 1] Compiling Hypotenuse ( Hypotenuse.hs, interpreted )
Ok, 1 module loaded.
*Hypotenuse>
Our code works as we'd expect, with the change that hypotenuse now has the more restrictive type we declared.
*Hypotenuse> hypotenuse 3 4
5.0
*Hypotenuse> :t hypotenuse
hypotenuse :: Double -> Double -> Double
One final change, albeit an extremely pedantic one, is to note the duplication of code, the ^2 part. Duplicated code is a bad thing, because it is often very difficult to keep it all in sync. Codebases evolve over time, and divergent evolution of duplicated functions leads to unnecessary complication and size. But we'll illustrate how to deal with this by adding a square function:
-- | A module for working with triangles.
module Hypotenuse where
-- | Compute the length of the hypotenuse of a triangle from the lengths
-- of its sides.
hypotenuse :: Double -> Double -> Double
hypotenuse a b = sqrt (square a + square b)
-- | Square a number.
square :: Num n => n -> n
square x = x ^ 2
Note that in this case, we decided to go with a more general type for square. Note as well that our definition of square follows its use. This is not a problem (it would be in some languages), as Haskell considers all the definitions in a module when it does its type analysis.
One of the nice things about abstracting out duplicate code is that it often makes it worthwhile for us to think about alternative implementations, e.g.,
square x = x * x
which won't make a perceptible difference here, but may in more complicated contexts.
The use of Haddock comments enables us to produce nicely formatted documentation, cf. Hypotenuse Documentation. We'll cover how to do this later.
A final remark for today: Haskell programmers care a lot about code quality. The language itself facilitates surprisingly rapid development, but this doesn't mean that real-world Haskell programmers knock off early to hit the bars. They are far more likely continue working on their code after it meets its specifications, looking for ways to make it more robust, more general, and more concise. This “tending of the garden” pays huge dividends over time.
*Exercise 1.2 The law of cosines is a generalization of the Pythagorean Theorem, which allows us to compute the length c of the third side of a triangle, given the lengths of the two other sides a and b, and the included angle γ.
Expand the Haskell script file Hypotenuse.hs to include a function law_of_cosines which takes three arguments: a, b, and gamma, and returns the length of c.
Some notes: your function should take the angle gamma in degrees, but you need to be aware that the Haskell's built in cos function expects its argument to be in radians, i.e.,
> cos pi
-1
Note that pi is a predefined constant in Haskell for the mathematical constant π.
Floating point arithmetic in Haskell (like almost all programming languages) is finite precision, and only approximately corresponds to the real numbers of mathematics. My implementation returned the following results, which you might want to use as test data:
> law_of_cosines 1 1 60
0.9999999999999999
> law_of_cosines 1 1 120
1.7320508075688772
> law_of_cosines 3 4 90
5.0
> law_of_cosines 3 4 0
1.0
> law_of_cosines 3 4 180
7.0
Exercise 1.3 If you have a mathematical turn of mind, you may find the optional lecture on Peano Arithmetic interesting.